





Next: 平均積分二乗誤差及びコスト関数の導入
Up: 方法
Previous: 方法
Contents
Index
長さ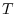 の時間依存Poisson過程のレート(強度過程)を
の時間依存Poisson過程のレート(強度過程)を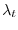 (
(![$t\in[0, \, T]$](img7.gif) )とする.
区間
)とする.
区間![$[0,\, \Delta]$](img8.gif) の棒ヒストグラムの真の高さは
の棒ヒストグラムの真の高さは
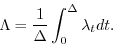 |
(1) |
で与えられる. この区間内の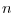 回の試行数の総スパイク数
回の試行数の総スパイク数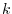 は次のPoisson分布で与えられる.
は次のPoisson分布で与えられる.
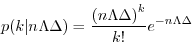 |
(2) |
従って 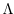 の不偏推定量である
の不偏推定量である
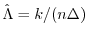 がデータから求められるヒストグラムの高さである.
がデータから求められるヒストグラムの高さである.





Next: 平均積分二乗誤差及びコスト関数の導入
Up: 方法
Previous: 方法
Contents
Index
hideaki
2006-07-11